Answer:
v₀ = 60.38 mi / h
With this stopping distance, the starting speed should have been 60.38 mi/h, which is much higher than the maximum speed allowed.
Step-by-step explanation:
For this exercise let's start by using Newton's second law
Y axis
N-W = 0
N = W
X axis
fr = m a
the expression for the friction force is
fr = μ N
we substitute
μ mg = m a
μ g = a
calculate us
a = 0.620 9.8
a = 6.076 m / s²
now we can use the kinematics relations
v² = v₀² - 2 a x
suppose v = 0
v₀ =
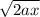 Ra 2ax
Ra 2ax
let's calculate
v₀ =
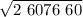
v₀ = 27.00 m / s
let's slow down to the english system
v₀ = 27.0 m / s (3.28 ft / 1m) (1 mile / 5280 ft) (3600s / 1h)
v₀ = 60.38 mi / h
With this stopping distance, the starting speed should have been 60.38 mi/h, which is much higher than the maximum speed allowed.