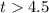Question:
At midnight, the temperature in a city was 5 degrees Celsius. The temperature was dropping at a steady rate of 2 degrees Celsius per hour.
Write an inequality that represents t, the number of hours past midnight, when the temperature was colder than -4 degrees Celsius. Explain or show your reasoning.
Answer:
Explanation:
Given
Let T = temperature and t = hours past midnight
So, we have:
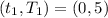 --- at midnight
--- at midnight
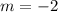 --- rate (it is negative because the temperature drops)
--- rate (it is negative because the temperature drops)
Required
Determine the inequality when the temperature is colder than -4 degrees
First, we calculate the hours when the temperature at -4 degrees
This is represented as:
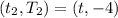
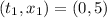
Using the slope formula, we have:
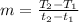
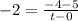
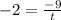
Solve for t
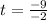
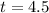
This implies that: at 4.5 hours, the temperature is at -4 degrees Celsius.
So, the inequality is: