Question

Low concentrations of EDTA near the detection limit gave the following dimensionless instrument readings: 175, 104, 164, 193, 131, 189, 155, 133, 151, and 176. Ten unknowns have a mean reading of 60.0. The slope of the calibration curve is 1.75×109M−1.

a) Estimate the signal detection limit for EDTA.
b) What is the concentration detection limit?
c) What is the lower limit of quantitation?

Answer 1

Following are the solution to these question:

Step-by-step explanation:

Calculating the mean:

`\bar{x}=(175+104+164+193+131+189+155+133+151+176)/(10)\\\\`

`=(1571)/(10)\\\\=157.1`

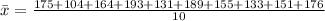
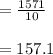
Calculating the standardn:

`\sigma=\sqrt{\frac{\Sigma(x_i-\bar{x})^2}{n-1}}\\\\`

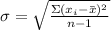
Please find the correct equation in the attached file.

`=28.195`

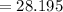
For point a:

`=3s+yblank \\\\=3 * 28.195+50\\\\=84.585+50\\\\=134.585\\`

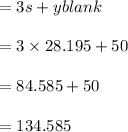
For point b:

`=3 \ (s)/(m)\\\\ = ((3 * 28.195))/(1.75 * 10^9 \ M^(-1))\\\\= 4.833 * 10^(-8) \ M`

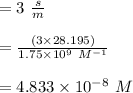
For point c:

`= 10 (s)/(m) \\\\= ((10 * 28.195))/(1.75 x 10^9 \ M^(-1))\\\\ = 1.611 * 10^(-7)\ M`

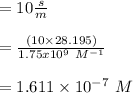
It is calculated by using the slope value that is
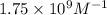`1.75 * 10^9 M^(-1)`. The slope value
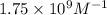`1.75 * 10^9 M^(-1)`is ambiguous.