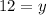Answer:
D) y = 12
Explanation:
One can use the angle bisector theorem to solve this problem. The angle bisector theorem states:
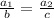
Where (
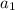 ) and (
) and (
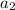 ) are a part of the side that is intersected by the angle bisector and (
) are a part of the side that is intersected by the angle bisector and (
 ) and (
) and (
 ) are the other two sides in the triangle. Substitute in the given values and solve for the unknown.
) are the other two sides in the triangle. Substitute in the given values and solve for the unknown.
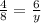
Simplify,
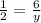
Cross products,