Question

Can somebody please help me with this question i attached the photo from khan academy.

Thank you!

Answer 1

Explanation:

In rectangle the diagonals bisect each other. So,O is the midpoint of AC

`Midpoint = \left((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2) \right)\\\\\\x_(1)=9 \ and \ y_(1)=6\\\\\left((9+x_(2))/(2),(6+y_(2))/(2) \right) = \left ((21)/(2),(19)/(2) \right)`

Compare the x- coordinates and y- coordinates

`(9+x_(2))/(2)=(21)/(2) \ ; \ (6+y_(2))/(2)=(19)/(2)\\\\\\9+x_(2)=(21)/(2)*2 \ ; \ 6 +y_(2)=(19)/(2)*2`

9 + x₂ = 21 ; 6 +y₂ = 19

x₂ = 21 -9 ; y₂ = 19 - 6

x₂ = 12 ; y₂ = 13

C(12 ,13)

Answer 2

C = (12, 13)

Explanation:

The centre of the rectangle is O.

Find the difference between the x and y-values of O and A:

`O_x-A_x=(21)/(2)-9=\frac32`

`O_y-A_y=(19)/(2)-6=\frac72`

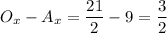
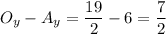
Now add those difference to the coordinates of O to find C:

x value of C =
`O_x+\frac32=(21)/(2)+\frac32=(24)/(2)=12`

y value of C =
`O_y+\frac72=(19)/(2)+\frac72=(26)/(2)=13`

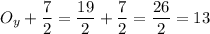
Therefore, the coordinates of C = (12, 13)