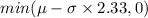Answer:
Var = 6.31
Explanation:
The Value at Risk (VAR)
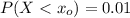
By using normal distribution
Mean
 = 10
= 10
Variance = 49
Standard deviation

This implies that:

Using the z-table;
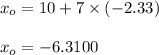
Hence, there exist 1% chance that X < -6.31 or the loss from investment is > 6.31
From the calculated value above;
 ; Since the result is negative, then it shows that the greater the value(i.e the positive or less negative it is ) the lower is the value of VAR. Thus, the least value of VAR is accepted by the largest value of
; Since the result is negative, then it shows that the greater the value(i.e the positive or less negative it is ) the lower is the value of VAR. Thus, the least value of VAR is accepted by the largest value of