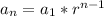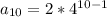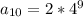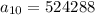Answer:
Geometric sequence
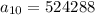
Explanation:
Given
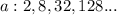
Solving (1): The type of sequence
To check for arithmetic sequence:
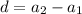 --- common difference
--- common difference

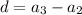
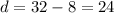
Both values of d are not the same; Hence, the sequence is not arithmetic
To check for geometric sequence:
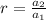 --- common ratio
--- common ratio
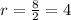
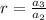
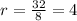
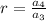
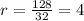
All values of r are the same.
Hence, it is a geometric sequence
Solving (2): Find
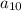
For a geometric sequence;