Suppose that the supply of x units of a product at price p dollars per unit is given by the following.
p = 20 + 90 ln(2x + 4)
(a) Find the rate of change of supply price with respect to the number of units supplied.
Answer:
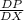
=
(b) Find the rate of change of supply price when the number of units is 38.
Answer: $ 2.25
(c) Approximate the price increase associated with the number of units supplied changing from 38 to 39.
ANSWER NEEDED: $