Question

Suppose that the supply of x units of a product at price p dollars per unit is given by the following.

p = 20 + 90 ln(2x + 4)

(a) Find the rate of change of supply price with respect to the number of units supplied.
Answer:
`(DP)/(DX)` =
`(90)/(x+2)`

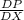
(b) Find the rate of change of supply price when the number of units is 38.
Answer: $ 2.25

(c) Approximate the price increase associated with the number of units supplied changing from 38 to 39.
ANSWER NEEDED: $

Answer 1

(a) dp/dx = 90/(x+2)

(b) $2.25

(c) approx = $2.25

exact = $2.22

Explanation:

`p = 20 + 90 \ln(2x + 4)`

(a) To find the rate of change, differentiate
`p` with respect to
`x` :

`\implies (d)/(dx)(p) = (d)/(dx)(20) + (d)/(dx)(90 \ln(2x + 4))`

`\implies (dp)/(dx)=0+90*(1)/(2x+4)*2`

`\implies (dp)/(dx)=(180)/(2x+4)`

`\implies (dp)/(dx)=(90)/(x+2)`

(b) Find
`(dp)/(dx)` when
`x=38` :

`\implies (dp)/(dx)=(90)/(38+2)`

`\implies (dp)/(dx)=(90)/(40)`

`\implies (dp)/(dx)=2.25`

(c) Approximate price increase associated with the number of units supplied changing from 38 to 39 is
`(dp)/(dx)` when
`x=38`

`\implies \$2.25`

Exact price increase:

`\implies \left. p \right_(x=39)-\left. p \right_(x=38)\\\\\implies [20 + 90 \ln(2 * 39 + 4)]-[20 + 90 \ln(2*38 + 4)]\\\\\implies 416.6047323...-414.3823972...\\\\\implies 2.222335133...\\\\\implies \$2.22`