Answer:
(a) -2.8
b) (1) Reject H0: p = 0.50 in favor of HA: p < 0.50; there is sufficient evidence to conclude that less than half of all UGA female students who, if they had a cell phone, would be willing to walk somewhere after dark that they would normally not go.
Explanation:
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
H0: p = 0.50
This means that:
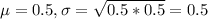
In a random sample of 305 UGA female students, 128 responded that, if they had a cell phone, they would be willing to walk somewhere after dark that they would normally not go.
This means that
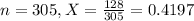
a) Value of the test statistic:

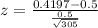

Pvalue:
We are testing the hypothesis that the proportion is less than 0.5, which means that the pvalue of the test is the pvalue of z = -2.81.
Looking at the z-table, z = -2.8 has a pvalue of 0.0026
(b) What is the correct conclusion for this hypothesis test at the 0.05 level of significance?
0.0026 < 0.05, which means that we reject the null hypothesis, that the proportion is 0.5, and accept the alternate hypothesis, that the proportion is less than 0.5, option (1).