Answer:
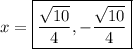
Explanation:
We can solve this question by using the method of finding the square root.
The given equation is:

Add 3 to both the sides of the equation.

Now, add 2 & 3 to get 5.
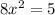
Dividing both the sides of the equation by 8, we get...
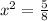
Now, take the square root of both the sides of the equation...
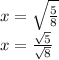
Rationalize the denominator.
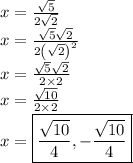

- The value of x =


Hope this helps!