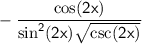Answer:
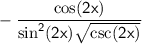
Explanation:
we are given a derivative
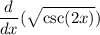
and said to figure out the first derivative
to do so
recall chain rule:
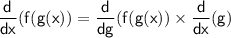
so we get
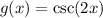
rewrite the derivative using the chain rule:
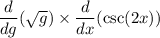
use square root derivative rule to simplify:
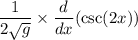
now we need to again use chain rule composite function derivative to simplify
where we'll take a new function n so we won't mess up two g's and we'll take 2x as n
use composite function derivative to simplify:
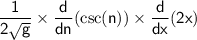
use derivative formula to simplify derivatives:
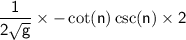
substitute the value of n:
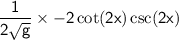
substitute the value of g:
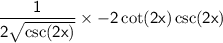
now we need our trigonometric skills to simplify
rewrite cot and csc:
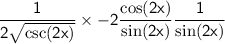
simplify multiplication:
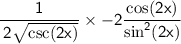
simplify multiplication: