Question

How many elements does A contains if it has 64 subsets​

Answer 1

Answer: 6

===========================================================

Step-by-step explanation:

Rule: If a set has n elements in it, then it will have 2^n subsets.

For example, there are n = 3 elements in the set {a,b,c}. This means there are 2^n = 2^3 = 8 subsets. The eight subsets are listed below.

1. {a,b,c} .... any set is a subset of itself
2. {a,b}
3. {a,c}
4. {b,c}
5. {a}
6. {b}
7. {c}
8. { } ..... the empty set

Subsets 2 through 4 are subsets with exactly 2 elements. Subsets 5 through 7 are singletons (aka sets with 1 element). The last subset is the empty set which is a subset of any set. You could use the special symbol
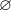`\varnothing` to indicate the empty set.

For more information, check out concepts relating to the power set.

-------------------

The problem is asking what value of n will make 2^n = 64 true.

You could guess-and-check your way to see that 2^n = 64 has the solution n = 6.

Another approach is to follow these steps.

`2^n = 64\\\\2^n = 2^6\\\\n = 6`

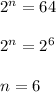
Which is fairly trivial.

Or you can use logarithms to solve for the exponent.

`2^n = 64\\\\\text{Log}\left(2^n\right)=\text{Log}\left(64\right)\\\\n*\text{Log}\left(2\right)=\text{Log}\left(64\right)\\\\n=\frac{\text{Log}\left(64\right)}{\text{Log}\left(2\right)}\\\\n\approx\frac{1.80617997398389} {0.30102999566399} \ \text{ ... using base 10 logs}\\\\n\approx5.99999999999983\\\\`

Due to rounding error, we don't land exactly on 6 even though we should.