1 Answer

Colincameron · Answer 1 · 2022-03-29T09:51:37+0000

Given:

Consider the given equation is:

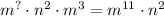
$m^?\cdot n^2\cdot m^3=m^(11)\cdot n^2$

To find:

The missing exponent.

Solution:

Let x be the missing exponent. Then the given equation can be written as

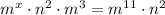
$m^x\cdot n^2\cdot m^3=m^(11)\cdot n^2$

It can be rewritten as:

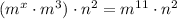
$(m^x\cdot m^3)\cdot n^2=m^(11)\cdot n^2$

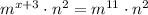
$m^(x+3)\cdot n^2=m^(11)\cdot n^2$
$[\because a^ma^n=a^(m+n)]$

On comparing the coefficient of m, we get

x+3=11

x=11-3

x=8

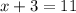
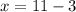
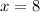
Therefore, the value of the missing exponent is 8. So, the complete equation is
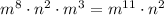$m^8\cdot n^2\cdot m^3=m^(11)\cdot n^2$ .

Please log in or register to add a comment.