Given:
The given function is:
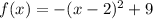
To find:
The transformations, intercepts and the vertex.
Solution:
The vertex form of a parabola is:
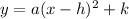 ...(i)
...(i)
Where, a is a constant and (h,k) is vertex.
If a<0, then the graph of parent quadratic function
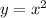 reflect across the x-axis.
reflect across the x-axis.
If h<0, then the graph of parent function shifts h units left and if h>0, then the graph of parent function shifts h units right.
If k<0, then the graph of parent function shifts k units down and if k>0, then the graph of parent function shifts k units up.
We have,
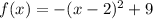 ...(ii)
...(ii)
On comparing (i) and (ii), we get
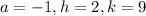
So, the graph of the parent function reflected across the x-axis, and shifts 2 units right and 9 units up.
Putting x=0 in (ii), we get
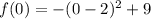
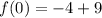

The y-intercept is 5.
Putting f(x)=0 in (ii), we get
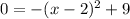
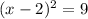
Taking square root on both sides, we get
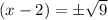
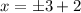
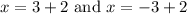
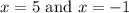
Therefore, the x-intercepts are -1 and 5.
The values of h and k are 2 and 9 respectively and (h,k) is the vertex of the parabola.
Therefore, the vertex of the parabola is (2,9).