Answer:

series diverges
Explanation:
To find the common ratio (r) of a geometric series, divide the (n+1)th term by the nth term.
When n = 1:
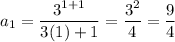
When n =2:
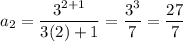
Therefore,
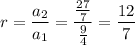
A series that converges has a finite limit. If |r| < 1, then the series will converge.
A series that diverges means either the partial sums have no limit or approach infinity. If |r| > 1 then the series diverges.
Therefore, as the limit of the series approaches infinity and it's r value is greater than 1, the series diverges.