Question

Helps me please help me please please help please help me please

Answer 1

`\boxed {\boxed {\sf (4,3) \ is \ not \ a \ solution}}`

Explanation:

If we want to test a solution, we can plug it into the equations and see if it checks out.

We are given the point (4,3). Since points are written (x,y)...

• x=4
• y=3

Substitute the values into the first equation.

`11x+9y=17 \\11(4)+9(3)=17`

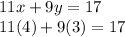
Multiply.

`44+ 27=17\\`

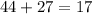
Add.

`71 \\eq 71`

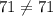
This does not check out, so we automatically know this point doesn't work. However, we can check the other equation.

`x+y=7 \\4+3=7\\7=7`

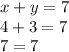
Even though the second equation works, BOTH have to work because this is a system of equations. Therefore, (4,3) is not a solution.