Answer:
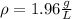
Step-by-step explanation:
Hello there!
In this case, since this imaginary gas can be modelled as an ideal gas, we can write:
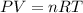
Which can be written in terms of density and molar mass as shown below:

Thus, by computing the pressure in atmospheres, the resulting density would be:
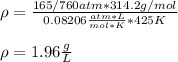
Best regards!