Answer:
We accept the null hypothesis, that is, the the mean amount of garbage per bin is not different from 50.
Explanation:
A sanitation supervisor is interested in testing to see if the mean amount of garbage per bin is different from 50.
This means that the null hypothesis is:
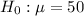
And the alternate hypothesis is:
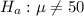
The test statistic is:
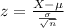
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
50 tested at the null hypothesis:
This means that
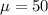
In a random sample of 36 bins, the sample mean amount was 50.67 pounds and the sample standard deviation was 3.9 pounds.
This means that
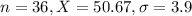
Value of the test statistic:
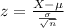
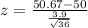
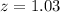
p-value:
Since we are testing if the mean is differente from a value and the z-score is positive, the pvalue is 2 multipled by 1 subtracted by the pvalue of z = 1.03.
z = 1.03 has a pvalue of 0.8485
1 - 0.8485 = 0.1515
2*0.1515 = 0.3030
0.3030 > 0.01, which means that we accept the null hypothesis, that is, the the mean amount of garbage per bin is not different from 50.