Question

6.167 High School Graduates. According to the document Cur-rent Population Survey, published by the U.S. Census Bureau, 30.4% of U.S. adults 25 years old or older have a high school degree as their highest educational level. If 100 such adults are selected at random, determine the probability that the number who have a high school degree as their highest educational level is

Answer 1

Hello your question is incomplete below is the missing value

determine the probability that the number who have a high school degree as their highest educational level is exactly 32

answer : P( x = 32 ) = 0.08

Explanation:

Given ;

n = 100 , p = 0.304

np = 100 * 0.304 = 30.4

n( 1 - p ) = 100 ( 1 - 0.304 ) = 69.6

applying normal approximation to the Binomial to determine mean value and standard deviation ( because: np and n(1-p) > 5 )

mean = np = 30.4

std =
`√(np(1-p))` =
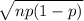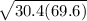`√(30.4(69.6))` = 4.6

Determine the probability of exactly 32

P( X = 32 ) = P( 31.5 < X < 32.5 )

= P( (31.5 - 30.4) / 4.6 < X < (32.5 - 30.4) / 4.6 )

= P ( 0.24 < Z < 0.46 )

= p( Z < 0.46 ) - p( Z< 0.24 ) ( using standard tables )

= 0.6772 - 0.5948 = 0.0824 ≈ 0.08