Question

In the late 2000's sales of SUVs decreased due to higher gas prices and improved alternative vehicles. A car dealer is interested whether it takes more days to sell SUV's vs. small cars. He gathers data from a sample of the most recent couple of months of sales and calculates that the he sold 18 SUV's with an average number of days to sale of 95 and a standard deviation of 32 days. For small cars, he sold 38 of them in an average of 48 days with a standard deviation of 24 days. The dealer wants to estimate how much longer it takes to sell an SUV vs. a small car by constructing a 95% confidence interval. 1. The facts of this problem are:

Answer 1

1. The facts are;

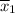`\overline x _1` = 95 days

s₁ = 32 days

n₁ = 18 SUV's

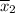`\overline x _2` = 48 days

n₂ = 38 small cars

s₂ = 24 days

The confidence level = 95%

The confidence interval is (29.55, 64.45)

Explanation:

The facts of the problem are;

The number of SUV's he sold, n₁ = 18 SUV's

The average number it took to sell the 18 SUV's,
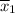`\overline x _1` = 95 days

The standard deviation of the time it took to sell the 18 SUV's, s₁ = 32 days

The number of small cars he sold, n₂ = 38 small cars

The average number it took to sell the 38 small cars,
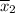`\overline x _2` = 48 days

The standard deviation of the time it took to sell the 38 small cars, s₂ = 24 days

The 95% confidence interval is given as follows;

Using a graphing calculator, we get, the critical-t,
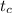`t_c` = 2.055529

`\left (\bar{x}_1-\bar{x}_(2) \right ) \pm t_(c) \cdot\sqrt{(s _(1)^(2))/(n_(1))+(s _(2)^(2))/(n_(2))}`

`\left (95-48 \right ) \pm 2.055529 * \sqrt{(32^(2))/(18)+(24^(2))/(38)}`

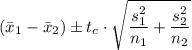
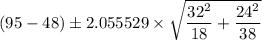
We get C.I. = 29.55259 < μ₁ - μ₂ < 64.44741

∴ C.I. ≈ 29.55 < μ₁ - μ₂ < 64.45