Answer:
Approximately
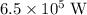 .
.
Step-by-step explanation:
At a speed of
 , the kinetic energy of the ride and the riders of mass
, the kinetic energy of the ride and the riders of mass
 (combined) would be:
(combined) would be:
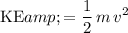 .
.
If friction is negligible,
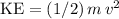 would be the work required to achieve this speed. That is:
would be the work required to achieve this speed. That is:
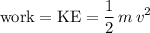 .
.
Given that this work was completed in a duration of
 , the average power would be:
, the average power would be:
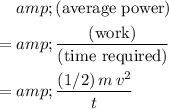 .
.
Substitute in
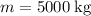 ,
,
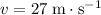 , and
, and
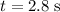 :
:
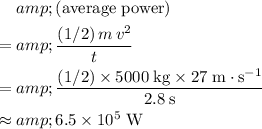 .
.
(Note that if acceleration is constant, the power input to the ride would be proportional to
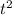 . The average power of input to the ride would be a quarter of the peak power input. Multiplying average velocity (proportional to
. The average power of input to the ride would be a quarter of the peak power input. Multiplying average velocity (proportional to
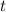 ) by average force (proportional to
) by average force (proportional to
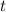 ) would overestimate the average power by
) would overestimate the average power by
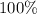 .)
.)