Question

If a ride at Disneyworld goes from rest to 27 m/s in 2.8 seconds and the mass of the ride and riders together is 5000 kg (true data!), what is the average power required to do this?

Answer 1

Approximately
`6.5 * 10^(5)\; {\rm W}`.

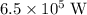Step-by-step explanation:

At a speed of
`v`, the kinetic energy of the ride and the riders of mass
`m` (combined) would be:

`\begin{aligned} \text{KE} &= (1)/(2)\, m\, v^(2)\end{aligned}`.

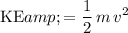If friction is negligible,
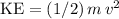`\text{KE} = (1/2)\, m\, v^(2)` would be the work required to achieve this speed. That is:

`\begin{aligned} \text{work} = \text{KE} = (1)/(2)\, m\, v^(2)\end{aligned}`.

Given that this work was completed in a duration of
`t`, the average power would be:

`\begin{aligned} & (\text{average power})\\ =\; & \frac{(\text{work})}{(\text{time required})} \\ =\; & ((1/2) \, m\, v^(2))/(t)\end{aligned}`.

Substitute in
`m = 5000\; {\rm kg}`,
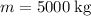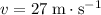`v = 27\; {\rm m\cdot s^(-1)}`, and
`t = 2.8\; {\rm s}`:

`\begin{aligned} & (\text{average power}) \\ =\; & ((1/2) \, m\, v^(2))/(t) \\ =\; & \frac{(1/2) * 5000\; {\rm kg} * 27\; {\rm m\cdot s^(-1)}}{2.8\; {\rm s}} \\ \approx \; & 6.5 * 10^(5)\; {\rm W}\end{aligned}`.

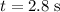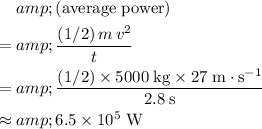(Note that if acceleration is constant, the power input to the ride would be proportional to
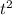`t^(2)`. The average power of input to the ride would be a quarter of the peak power input. Multiplying average velocity (proportional to
`t`) by average force (proportional to
`t`) would overestimate the average power by
`100\%`.)