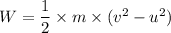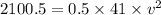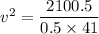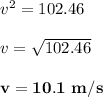Question

A 41.0-kg crate, starting from rest, is pulled across level floor with a constant horizontal force of 135 N. For the first 15.0 m the floor is essentially frictionless, whereas for the next 12.0 m the coefficient of kinetic friction is 0.320. (a) Calculate the work done by all the forces acting on the crate, during the entire 27.0 m path. (b) Calculate the total work done by all the forces. (c) Calculate the final speed of the crate after being pulled these 27.0 m.

Answer 1

Step-by-step explanation:

From the information given;

mass of the crate m = 41 kg

constant horizontal force = 135 N

where;

`s_1 = 15.0 \ m \\ \\ s_2 = 12.0 \ m`

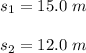
coefficient of kinetic friction
`u_k` = 0.28

a)

To start with the work done by the applied force
`(W_f)`

`W_F = F* (s_1 +s_2) * cos(0) \ J`

`W_F = 135 * (12 +15) * cos(0) \ J \\ \\ W_F = (135 * 37 )J \\ \\ W_F =4995 \ J`

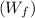
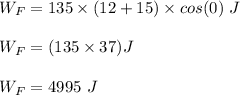
Work done by friction:

`W_(ff) = -\mu\_k* m * g * s_2 \\ \\ W_(ff) = -0.320 * 41 * 9.81 * 12 \ J \\ \\ W_(ff) = -1544.49 \ J`

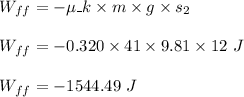
Work done by gravity:

`W_g = mg * (s_1+s_2) * cos (90)} \ J \\ \\ W_g = 0 \ j`

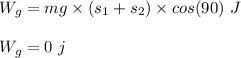
Work done by normal force;

`W_n = N * (s_1 + s_2) * cos (90) \ J`

`W_n = 0 \ J`

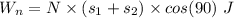
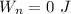
b)

total work by all forces:

`W = F * (s_1 + s_2) + \mu_k * m * g * s_2 * 180 \\ \\ W = 135 * (15+12) \ J - 0.320 * 41 * 9.81 * 12`

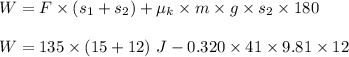
W = 2100.5 J

c) By applying the work-energy theorem;

total work done = ΔK.E

`W = (1)/(2)* m * (v^2 - u^2)`

`2100.5 = 0.5 * 41 * v^2`

`v^2 = (2100.5)/( 0.5 * 41 )`

`v^2 = 102.46 \\ \\ v = √(102.46) \\ \\ \mathbf{v = 10.1 \ m/s}`