Answer:
Step-by-step explanation:
From the information given:
oxidation of oxidized solution takes place at 950° C
For wet oxidation:
The linear and parabolic coefficient can be computed as:
![(B)/(B/A) = D_o \ exp \Big [(-\varepsilon a)/(k_BT) \Big]](https://img.qammunity.org/2022/formulas/chemistry/college/xxk1ez5oe5dk4ubmhrr67wtwe0fqt8gwx6.png)
Using
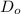 and
and
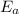 values obtained from the graph:
values obtained from the graph:
Thus;
![(B)/(A) = 1.63 * 10^8 exp \Big [ (-2.05)/(8.617 * 10^(_-5)* 1173)\Big] \\ \\ = 0.2535 \ \ \mu m/hr](https://img.qammunity.org/2022/formulas/chemistry/college/u17k465uptlq71eijhau55uwrkf3axljkf.png)
![B= 386 \ exp \Big [-(0.78)/(8.617 * 10^(-3) * 1173) \Big] \\ \\ = 0.1719 \ \mu m^2/hr](https://img.qammunity.org/2022/formulas/chemistry/college/cli4ov109i0nh1jpir2q3n5issndqgvsg5.png)
So, the initial time required to grow oxidation is expressed as:
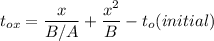
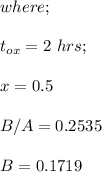
∴
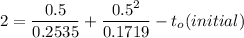
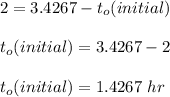
NOW;
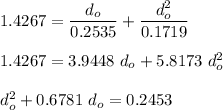
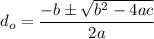
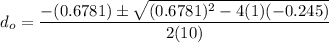
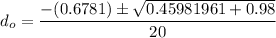
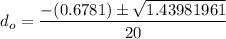
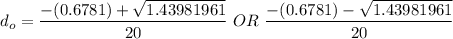
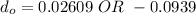
Thus; since we will consider the positive sign, the initial thickness
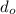 is ;
is ;
≅ 0.261 μm