Answer:
pH = 3.513
Step-by-step explanation:
Hello there!
In this case, since this titration is carried out via the following neutralization reaction:

We can see the 1:1 mole ratio of the acid to the base and also to the resulting acidic salt as it comes from the strong HCl and the weak hydroxylamine. Thus, we first compute the required volume of HCl as shown below:

Now, we can see that the moles of acid, base and acidic salt are all:

And therefore the concentration of the salt at the equivalence point is:
![[HONH_3^+Cl^-]=(0.0044mol)/(0.022L+0.0293L) =0.0858M](https://img.qammunity.org/2022/formulas/chemistry/college/3t9bgqsile1ltshiowv9pgif5own5l3fvl.png)
Next, for the calculation of the pH, we need to write the ionization of the weak part of the salt as it is able to form some hydroxylamine as it is the weak base:
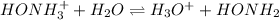
Whereas the equilibrium expression is:
![Ka=([H_3O^+][HONH_2])/([HONH_3^+])](https://img.qammunity.org/2022/formulas/chemistry/college/6nb399gcmuyuzdt3rzfzcsjjl7nxwpvai5.png)
Whereas Ka is computed by considering Kw and Kb of hydroxylamine:
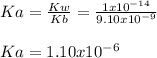
So we can write:
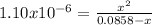
And neglect the x on bottom to obtain:
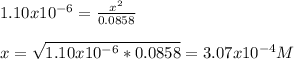
And since x=[H3O+] we obtain the following pH:
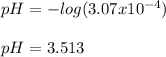
Regards!