Answer:
We accept the null hypothesis, that is, that the mean weight of the cans is still of 12 ounces of fruit.
Explanation:
Pineapple Corporation (PC) maintains that their cans have always contained an average of 12 ounces of fruit.
This means that the null hypothesis is:
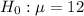
The production group believes that the mean weight has changed.
This means that the alternate hypothesis is:
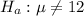
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
12 is tested at the null hypothesis:
This means that
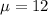
They take a sample of 15 cans and find a sample mean of 12.05 ounces and a sample standard deviation of .08 ounces.
This means, respectibely, that
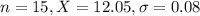
Value of the test statistic:

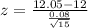
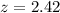
Pvalue of the test:
We are testing if the mean is different from a value, which means that the pvalue is 2 multiplied by 1 subtracted by the pvalue of z = 2.42.
Looking at the z-table, z = 2.42 has a pvalue of 0.9922
1 - 0.9922 = 0.0078
2*0.0078 = 0.0156
What conclusion can we make from the appropriate hypothesis test at the .01 level of significance?
0.0156 > 0.01. This means that at the 0.01 level, we accept the null hypothesis, that is, that the mean weight of the cans is still of 12 ounces of fruit.