Answer:
The minimum sample size we should anticipate using is 601.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
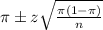
In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
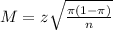
We have no history with this characteristic, so we have no idea as to what the proportion might be.
This means that we use
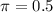 , which is when the largest sample size will be needed.
, which is when the largest sample size will be needed.
95% confidence level
So
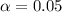 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
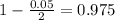 , so
, so
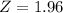 .
.
What is the minimum sample size we should anticipate using?
This is n for which M = 0.04. So
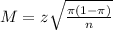
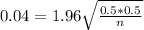
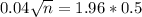
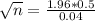
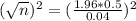
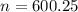
Rounding up, 601
The minimum sample size we should anticipate using is 601.