Answer:
We accept the null hypothesis, that is, that the population mean is not different from 0.7.
Explanation:
A brochure claims that the average maximum height a certain type of plant is 0.7 m.
This means that the null hypothesis is:
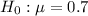
A gardener suspects that this estimate is not accurate locally due to soil conditions.
Hypothesis test to determine whether the population mean is different from 0.7m, which means that the alternate hypothesis is:
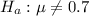
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.7 is tested at the null hypothesis:
This means that
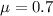
A random sample of 43 plants is taken. The mean height of the plants in the sample is 0.65m.
This means, respectively, that
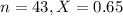
Assume that the population standard deviation is 0.2 m.
This means that
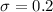
Value of the test statistic:


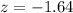
Pvalue of the test:
Since we are testing that the mean is different of a value, and z is negative, the pvalue of the test is 2 multiplied by the pvalue of z = -1.64
z = -1.64 has a pvalue of 0.0505
2*0.0505 = 0.101
Using a 1% level of significance, perform a hypothesis test to determine whether the population mean is different from 0.7m.
0.101 > 0.01, which means that we accept the null hypothesis, that is, that the population mean is not different from 0.7.