Answer:
a) 0.3333 = 33.33% probability that the low bid on the next intrastate shipping contract is below $25,000.
b) 0.1667 = 16.67% probability that the low bid on the next intrastate shipping contract is in excess of $28,000.
Explanation:
A distribution is called uniform if each outcome has the same probability of happening.
The uniform distribution has two bounds, a and b.
The probability of finding a value lower than x is given by:
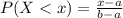
The probability of finding a value higher than x is given by:

Uniformly distributed between 23 and 29
This means that
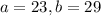
(a) Find the probability that the low bid on the next intrastate shipping contract is below $25,000.
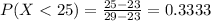
0.3333 = 33.33% probability that the low bid on the next intrastate shipping contract is below $25,000.
(b) Find the probability that the low bid on the next intrastate shipping contract is in excess of $28,000.

0.1667 = 16.67% probability that the low bid on the next intrastate shipping contract is in excess of $28,000.