Hello!
Let's consider what the question asks for:
==> equation of tangent line to y = 3sin(x)
--> at: x = 5π/4
To find the slope of the line at a specific point on the function
--> MUST find the derivative of equation
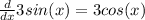
Derivative is function to find slope of function at every specific point
--> let's find the slope at x = 5π/4
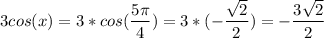
Now that we found the slope, we must also find the point at which the tangent line touches the function
--> simply plug x = 5π/4' to find y
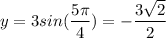
--> thus our point which the tangent line and function touch is
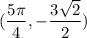
Now let's write our tangent line's equation in point-slope form:
 <== Answer
<== Answer