Question

The perimeter of an equilateral triangle is 12\/3 cm. Find the radius, apothem and area of the equilateral triangle.

Answer 1

Radius - 4

Apothem - 2

Area -
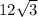`12√(3)` or 20.8

Explanation:

Try to draw out my explanation so you know what this looks like.

~~~~

This is an equilateral triangle, so all sides are the same length. The perimeter can be divided by 3 to get each side length...

`12√(3) /3 = 4√(3)`

Now that we know the side lengths, we can get this started!

~~~~

Now, an equilateral triangle has angles that all equal 60 degrees. We can bisect this into TWO special case triangles of measures 90-60-30.

4 times the square root of 3 will be the hypotenuse, and the smallest leg is always half of that. The larger leg is represented as the small leg times the square root of 3.

`Small=2√(3) \\Hypotenuse = 4√(3) \\Long =6`

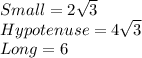
By the way, the formula for the area can be either of the two:

`A= (1)/(2) bh\\or\\A = (1)/(2) NAS`

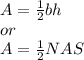
we can easily find the area using the first formula.

`A= (1)/(2) (4√(3) )(6)\\A=12√(3)`

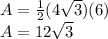
The radius is the distance from the center to the corners & the apothem is the distance from the center to a side...

So we can divide the big triangle into a mini triangle at the bottom left/right

The height (small leg) of that triangle would be the apothem

The hypotenuse of that triangle would be the radius.

I did the math really quick because this is getting long. Anyhow, the small leg is 2 so is the apothem, and the hypotenus is 4, so is the radius

Happy April Fool's btw, lol.