Answer:
The time it takes for the change in the angular velocity to occur is 6.5 seconds
Step-by-step explanation:
From the question, we have;
The angular acceleration of the wheel, α = -4.20 rad/s²
The final angular velocity of the wheel, ω = -26.0 rad/s
From the information, we have the initial direction of rotation of the wheel = Counterclockwise
The angular displacement while the change occurs = 0 rad/s
Therefore, the initial angular velocity of the wheel, ω₀ = 0 rad/s
We have;
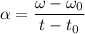
Where;
t - t₀ = The time it takes for the change to occur
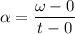
When t₀ = 0, we have;
t - t₀ = t
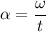
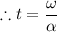
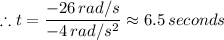
The time it takes for the change in the angular velocity to occur is t - t₀ = 6.5 seconds