Answer:
Don Abel debe construir un cuadrado con lados de 25 metros de longitud.
Explanation:
Geométricamente hablando, el área y el perímetro del rectángulo rodeado por el cerco son representadas por las siguientes fórmulas:
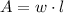 (1)
(1)
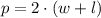 (2)
(2)
Donde:
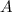 - Área, en metros cuadrados.
- Área, en metros cuadrados.
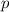 - Perímetro, en metros.
- Perímetro, en metros.
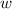 - Ancho, en metros.
- Ancho, en metros.
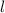 - Longitud, en metros.
- Longitud, en metros.
Puesto que el área a cercar debe ser la máxima posible y la longitud disponible de malla es de 100 metros, cabe despejar el ancho en (2):
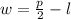
Ahora, aplicamos esta expresión en (1) y expandimos la expresión resultante:
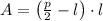
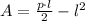 (3)
(3)
A continuación, obtenemos la primera y segunda derivada de (3):
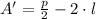 (4)
(4)
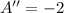 (5)
(5)
Igualando (4) a cero, tenemos que el valor crítico de la longitud del rectángulo es:
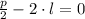
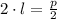
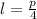
Por (5), sabemos que ese valor crítico está asociado al área máxima.
Si sabemos que
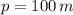 , entonces la longitud del rectángulo es:
, entonces la longitud del rectángulo es:
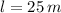
Ahora, tenemos el ancho de la figura por (2):
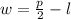
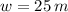
En consecuencia, don Abel debe construir un cuadrado con lados de 25 metros de longitud.