Answer:
The area of the rectangle is increasing at a rate of 168 square centimeters per second.
Explanation:
Geometrically speaking, the area of a rectangle (
 ), in square centimeters, is described by following expression:
), in square centimeters, is described by following expression:
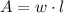 (1)
(1)
Where:
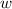 - Width, in centimeters.
- Width, in centimeters.
 - Height, in centimeters.
- Height, in centimeters.
By Differential Calculus, we find an expression for the rate of change of the area of the rectangle (
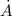 ), in square centimeters per second:
), in square centimeters per second:
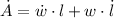 (2)
(2)
Where:
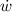 - Rate of change of the width of the rectangle, in centimeters per second.
- Rate of change of the width of the rectangle, in centimeters per second.
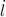 - Rate of change of the length of the rectangle, in centimeters per second.
- Rate of change of the length of the rectangle, in centimeters per second.
If we know that
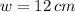 ,
,
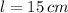 ,
,
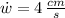 and
and
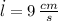 , then the rate of change of the area of the rectangle is:
, then the rate of change of the area of the rectangle is:
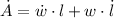
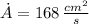
The area of the rectangle is increasing at a rate of 168 square centimeters per second.