Answer:
1)
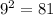
2)
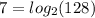
Explanation:
1)
We need to use the property of power and logarithms, particularly this:
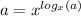 (1)
(1)
So, let's take take the exponent:
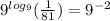
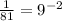
now, we can write the negavitve power as:
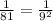
So, the aswer will be:
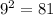
2)
Applying equation 1, let's take log in base 2 on each side of the equation
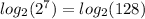
using the power definition in log, we have:
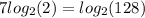
Therefore, the answer is:
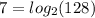
I hope it helps you!