Given:
The quadratic equation is
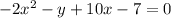
To find:
The vertex of the given quadratic equation.
Solution:
If a quadratic function is
 , then
, then
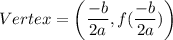
We have,
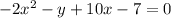
It can be written as
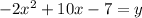
 ...(i)
...(i)
Here,
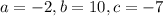 .
.
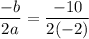
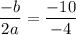
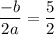
Putting
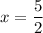 in (i), we get
in (i), we get
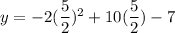
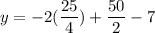

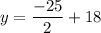
On further simplification, we get
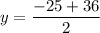
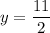
So, the vertex of the given quadratic equation is
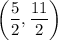 .
.
Therefore, the correct option is A.