Question

Find the area of the kite

Answer 1

Given:

A figure of a kite.

To find:

The area of the given kite.

Solution:

The area of a kite is the half of the product of its diagonals.

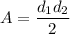`A=(d_1d_2)/(2)` ...(i)

Where,
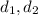`d_1,d_2` are two diagonals of the kite.

From the given figure it is clear that the length of one diagonal is the sum of 12 and 8.

`d_1=12+8`

`d_1=20`

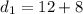
Let the second diagonal be 2x. The first diagonals bisect the second diagonal. So, the length of one parts of the diagonal is x.

Diagonals of a kite are perpendicular to each other. Using Pythagoras theorem, we get

`Hypotenuse^2=Perpendicular^2+Base^2`

`13^2=x^2+12^2`

`169-144=x^2`

`25=x^2`

`5=x`

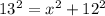
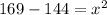
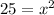
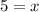
The length of second diagonal is:

`d_2=2x`

`d_2=2(5)`

`d_2=10`

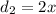
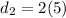
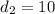
Substituting
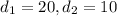`d_1=20,d_2=10` in (i), we get

`A=(20* 10)/(2)`

`A=(200)/(2)`

`A=100`

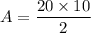
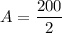
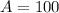
Therefore, the area of the kite is 100 square units.