Given:
Line ST is perpendicular to line PR.
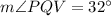
To find:
The measure of angle SQU.
Solution:
Line ST is perpendicular to line PR.
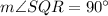
If two lines intersect each other, then the vertically opposite angles are equal.
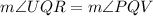 (Vertically opposite angle)
(Vertically opposite angle)
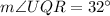
Now,
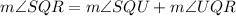
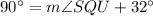
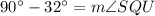
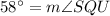
Therefore, the correct option is D.