Answer:

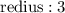
Explanation:
we are given a circle equation
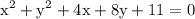
we want to figure out the centre and the redious of the circle from the equation notice that the given circle equation is in general form given by

general form of circle equation is a simplified version of standard form. the standard form of circle equation is given by:
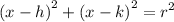
where:
- (h,k) is the centre
- r is the redious
notice that the there're two completed squares in the standard form therefore we can consider completing square to figure out the centre and the redious
indentifying centre and redious:
rearrange:
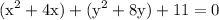
cancel 11 from both sides:

add 4 to the both sides so that the equality don't affect:
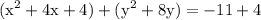
simplify addition:
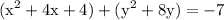
once again to complete the square add 16 to both sides which yields:

complete the squares by using (a+b)²=a²+2ab+b² pattern:
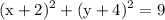
we can still rewrite it to figure out the redious and the centre:
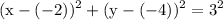
therefore we obtain:
- centre:(h,k)=(-2,-4)
- redious:r=3
and we are done!