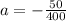Answer:

Explanation:
Given
See attachment for graph
Required
Write the vertex form and then solve for
The general equation is:
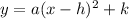
From the attachment, the vertex is at:
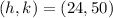
i.e.
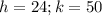
Considering point:
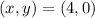
i.e.
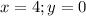
Substitute these values in
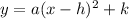
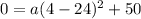
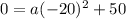
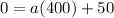
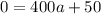
Solve for a

Make a the subject