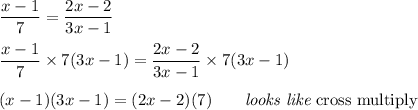Question

Anyone can help me solve this equation using cross multiplying

Answer 1

9514 1404 393

Answer:

x = 1 or 5

Explanation:

The notion of "cross-multiplying" is the idea that the numerator on the left is multiplied by the denominator on the right, and the numerator on the right is multiplied by the denominator on the left. This looks like ...

`\displaystyle (x-1)/(7)=(2x-2)/(3x-1)\ \longrightarrow\ (x-1)(3x-1)=(7)(2x-2)`

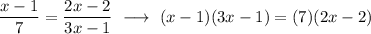
Then the solution proceeds by eliminating parentheses, and solving the resulting quadratic equation.

`3x^2-4x+1=14x-14\\\\3x^2-18x+15=0\qquad\text{subtract $14x-14$}\\\\x^2-6x+5=0 \qquad\text{divide by 3}\\\\(x-1)(x-5)=0\qquad\text{factor}\\\\x\in\{1,5\}`

_____

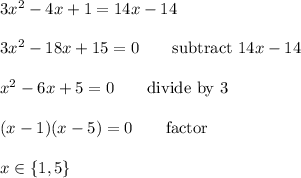
Comment on "cross multiply"

Like a lot of instructions in Algebra courses, the idea of "cross multiply" describes what the result looks like. It doesn't adequately describe how you get there. The one and only rule in solving Algebra problems is "whatever is done to one side of the equation must also be done to the other side of the equation." If you multiply one side by one thing and the other side by a different thing, you are violating this rule.

What looks like "cross multiply" is really "multiply by the product of the denominators and cancel like terms from numerator and denominator." Here's what that looks like with the intermediate steps added.

`\displaystyle (x-1)/(7)=(2x-2)/(3x-1)\\\\(x-1)/(7)*7(3x-1)=(2x-2)/(3x-1)*7(3x-1)\\\\(x-1)(3x-1)=(2x-2)(7)\qquad\textit{looks like}\text{ cross multiply}`