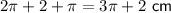Answer:
ABC shaded area = 36
 - 72 cm²
- 72 cm²
ABC shaded area perimeter =
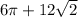 cm
cm
ABCD area =
 cm²
cm²
ABCD perimeter =
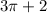 cm
cm
Explanation:
Shape ABC
Assuming you want the area and perimeter of the shaded part of the shape only...
Area
Area of a sector =
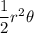 (where r is the radius and
(where r is the radius and

⇒ area of a sector =
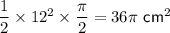
Area of triangle = 1/2 x base x height
⇒ area of triangle = 1/2 x 12 x 12 = 72 cm²
Therefore, area of shaded area = area of sector - area of triangle
⇒ area = 36
 - 72 cm²
- 72 cm²
Perimeter
Arc length =
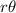 (where r is the radius and
(where r is the radius and

⇒ arc length =
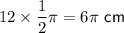
Hypotenuse of triangle =
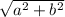 (where a and b are the legs of the right triangle)
(where a and b are the legs of the right triangle)
⇒ hypotenuse =
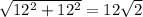 cm
cm
Therefore, perimeter = arc length + hypotenuse
⇒ perimeter =
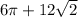 cm
cm
Shape ABCD
Area
Area of a semicircle =
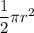 (where r is the radius)
(where r is the radius)
⇒ area of large semicircle ABC =
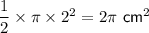
⇒ area of small semicircle AD =
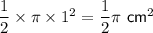
⇒ area of shape ABCD =
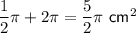
Perimeter
1/2 circumference =
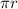
⇒ perimeter =