Answer:
A.
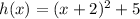
Explanation:
First, we need to defined the two transformations required to derive
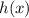 .
.
Vertical translation
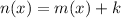 ,
,
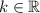 (1)
(1)
Where:
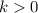 , upwards.
, upwards.
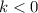 , downwards.
, downwards.
Horizontal translation
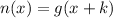 ,
,
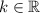 (2)
(2)
Where:
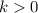 , leftwards.
, leftwards.
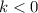 , rightwards.
, rightwards.
Let
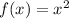 , if
, if
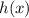 is translated 2 units left and 5 units up, then we have the resulting expression:
is translated 2 units left and 5 units up, then we have the resulting expression:
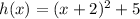 (3)
(3)
Hence, correct answer is A.