Given:
The expression is
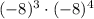
To find:
The expression in repeated multiplication form and then write the expression as a power.
Solution:
We have,
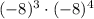
The repeated multiplication form of this expression is
![=[(-8)\cdot (-8)\cdot (-8)]\cdot [(-8)\cdot (-8)\cdot (-8)\cdot (-8)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ihkijldqxelcnoayyr6pd6fyprw80fovh0.png)
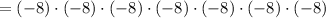
Clearly, (-8) is multiplied seven times by itself. So,
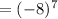
Therefore, the repeated multiplication form of the given expression is
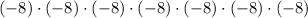 and the expression as single power is
and the expression as single power is
 .
.