Answer:
Velocity of the car at the bottom of the slope: approximately
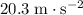 .
.
It would take approximately
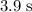 for the car to travel from the top of the slope to the bottom.
for the car to travel from the top of the slope to the bottom.
Step-by-step explanation:
The time of the travel needs to be found. Hence, make use of the SUVAT equation that does not include time.
- Let
 denote the final velocity of the car.
denote the final velocity of the car. - Let
 denote the initial velocity of the car.
denote the initial velocity of the car. - Let
 denote the acceleration of the car.
denote the acceleration of the car. - Let
 denote the distance that this car travelled.
denote the distance that this car travelled.
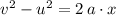 .
.
Given:
Rearrange the equation
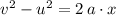 and solve for
and solve for
 :
:
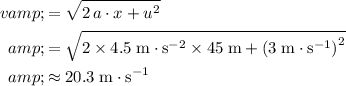 .
.
Calculate the time required for reaching this speed from
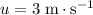 at
at
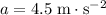 :
:
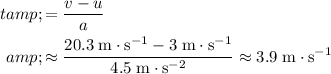 .
.