Answer:
Explanation:
1). In ΔABC,
For angle A as a reference angle,
Opposite side of ∠A → BC
Adjacent side of ∠A → AC
Hypotenuse → AB
2). By using tangent ratio in ΔYWZ,
tan(72°) =
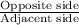
tan(72°) =
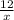
x =
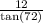
x = 3.899
x ≈ 3.9
3). By using sine rule in ΔKNM,
tan(x°) =
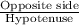
tan(x) =
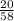
x =
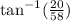
x = 19.03
x ≈ 19.0°
4). By applying cosine ratio in ΔJKF,
tan(70°) =
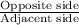
tan(70) =
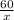
x =
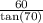
x = 21.838
x ≈ 21.8