Question

What are the mean, variance, and standard deviation of these values? Round to the nearest tenth. 12, 13, 15, 4, 11, 12

Plz help

Answer 1

i. Mean = 11.2

ii. Variance = 14.17

iii. Standard deviation = 3.76

Explanation:

i. Mean, m =
`(sum of the values)/(number of the values)`

=
`(4+11+12+12+13+15)/(6)`

=
`(67)/(6)`

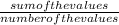
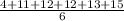
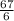
= 11.2

The mean of the given data is 11.2

ii. Variance =
`(sum(x_(i) - m)^(2))/(n-1)`

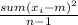
where:
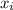`x_(i)` is the value of the one observation, m is the sample mean and n is the number of data given.

=
`([(4-11.2)^(2)+(11-11.2)^(2) + (12-11.2)^(2) + (12-11.2)^(2) + (13-11.2)^(2) + (15-11.2)^(2)] )/(6-1)`

=
`([51.84+0.04+0.64+0.64+3.24+14.44])/(5)`

=
`(70.84)/(5)`

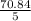
= 14.168

Variance = 14.17

iii. Standard deviation =
`√(Variance)`

=
`√(14.17)`

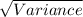
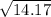
= 3.76