Question

The following function describes the number of employees working at a company, In thousands, where trepresents the number of years since the company revised the benefits package.

f(t) = 1.5(0.90)^t

Answer 1

Consider the missing part of the question is "Select the correct statement.

A. The number of employees is increasing by 50% every year.

B. The number of employees is decreasing by 10% every year.

C. The number of employees is decreasing by 90% every year.

D. The number of employees is increasing by 90% every year."

Given:

The function is:

`f(t)=1.5(0.90)^t`

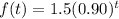
Where, f(t) is the number of employees working at a company, in thousands and t is the number of years since the company revised the benefits package.

To find:

The correct statement from the given options.

Solution:

The general exponential decay model is:

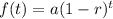`f(t)=a(1-r)^t` ...(i)

Where, a is the initial value, r is the rate of decay and t is the number of years.

We have,

`f(t)=1.5(0.90)^t`

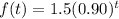
It can be written as

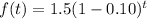`f(t)=1.5(1-0.10)^t` ...(ii)

From (i) and (ii), we get

`a=1.5,r=0.10`

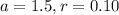
The initial value is 1.5 and the rate of decay is 0.10 or 10%. It means the number of employees is decreasing by 10% every year.

Therefore, the correct option is B.