Answer:
pH = 11.216.
Step-by-step explanation:
Hello there!
In this case, according to the ionization of ammonia in aqueous solution:
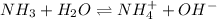
We can set up its equilibrium expression in terms of x as the reaction extent equal to the concentration of each product at equilibrium:
![Kb=([NH_4^+][OH^-])/([NH_3]) \\\\1.80x10^(-5)=(x*x)/(0.150-x)](https://img.qammunity.org/2022/formulas/chemistry/college/cvpfwgr2a7026jt5v4dms6gq6hs0g9lilc.png)
However, since Kb<<<1 we can neglect the x on bottom and easily compute it via:
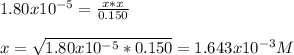
Which is also:
![[OH^-]=1.643x10^(-3)M](https://img.qammunity.org/2022/formulas/chemistry/college/swm2itinnvgyz679rz3y8sruevbbdomr9c.png)
Thereafter we can compute the pOH first:
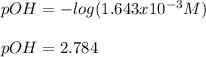
Finally, the pH turns out:
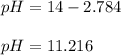
Regards!